时间序列异常检测调研

在智能运维领域，需要监控很多的指标，无论是与硬件、与系统相关的系统监控指标，还是各种与业务相关的指标。很多的系统异常就是通过这些监控指标检测出来的。所以分析处理时间序列数据，找出异常还是很重要的。分析方法主要有以下几种。

1. 移动平均（Moving Average，MA）

移动平均是一种分析时间序列的常用工具，它可过滤高频噪声和检测异常点。根据计算方法的不同，常用的移动平均算法包括简单移动平均、加权移动平均和指数移动平均。假设移动平均的时间窗口为T，有一个时间序列：

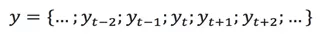
1.1  简单移动平均（Simple Moving Average，SMA）

在序列取值随时间波动较小的场景中，可以用历史值的均值作为当前值的预测值。

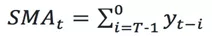
上述移动均值与该时刻的真实值的差值超过一定阈值则判定该时间的值异常。

这种方法适用于：

a. 对噪声数据进行平滑处理时，即用移动均值替代当前时刻取值以过滤噪声；

b. 在取值随时间波动较小时，预测未来的取值。

1.2  加权移动平均（Weighted Moving Average, WMA）

由于简单移动平均对窗口内所有的数据点都给予相同的权重，对近期的最新数据不够敏感，预测值存在滞后性。所以如果给近期的数据更高的权重，就能更快的捕捉近期的变化，加权移动平均和指数移动平均就是基于这样的想法。

加权移动平均比简单移动平均对近期的变化更加敏感，滞后性小于简单移动平均。但由于仅采用线性权重衰减，加权移动平均仍然存在一定的滞后性。

1.3  指数移动平均（Exponential Moving Average, EMA）

指数移动平均和加权移动平均类似，但不同之处是各数值的加权按指数递减，而非线性递减。此外，在指数衰减中，无论往前看多远的数据，该期数据的系数都不会衰减到 0，而仅仅是向 0 逼近。因此，指数移动平均实际上是一个无穷级数，即无论多久远的数据都会在计算当期的指数移动平均数值时，起到一定的作用，只不过离当前太远的数据的权重非常低。在实际应用中，可以按如下方法得到t时刻的指数移动平均：

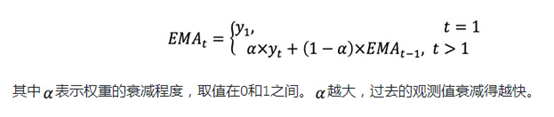
2. 同比和环比

图1 同比环比示意图

同比和环比计算公式如图1所示。适合数据呈周期性规律的场景中。当上述比值超过一定阈值则判定出现异常。

3. 时间序列分解

时间序列分解（STL，Seasonal and Trend decomposition using Loess）是分析时间序列的常用方法。对于存在季节性因素的时间序列，我们可以将其分解为趋势项、季节项和残差项，如图2所示，其中趋势项主要捕捉长期变化，季节项捕捉周期性变化，而残差项则捕捉那些不能被趋势或季节效应解释的变化。对时间序列进行分解后，可以针对分解出的季节项和趋势项分别进行分析和预测。

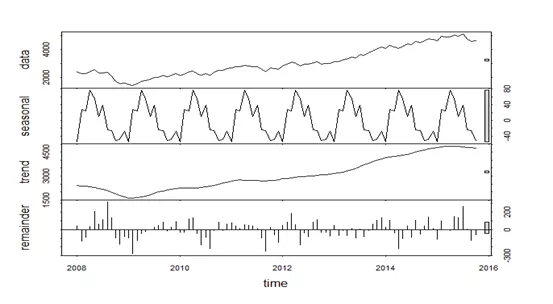
图2 STL分解示意图

在做数据分解时，首先需要明确，数据的周期，是一天，还是一年，如果对数据周期性不确定的，可以通过傅里叶变换计算数据周期。

在做分解时，有两种方式可以选择，一个是加法方式，一个是乘法方式。其中：

1)       加法方式：原始数据 = 平均季节数据 + 趋势数据 + 残差

这种方式，随着时间的推移季节数据不会有太大的变化。

2)       乘法方式：原始数据 = 季节数据 * 趋势数据 * 残差

这种方式，直观感受是随着时间的推移季节数据波动会非常明显。

分解之后，数据如果有异常，就会体现在残差数据集中。找出残差数据集的异常可以采用n-sigma方法，确认残差数据满足正太分布，或者近似正太分布，可以计算出残差数据集的标准差，常规方式是数据点与均值的差值绝对值在3倍标准差外，则认为是异常点，也就是3-sigma方案。也有例外，图3的残差数据集可能不能被上述方法将异常检测出来，这段数据连续几分钟都是在3倍标准差内，但是出现这种的可能性为（1-99.7%）^n，这种情况出现的概率相当低，如果出现也应该被识别为异常点。

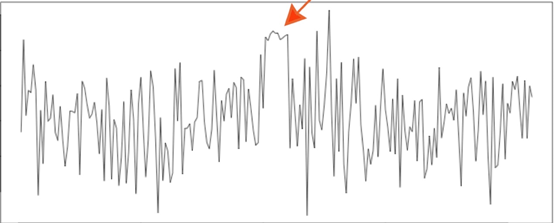
图3 残差数据集异常

4. 指数平滑

当数据在时间轴上可能呈现一定的稳态或者规律，利用过去时间区间的值来预测未来的值也是时序检测方法之一，即指数平滑法。

将指数平滑法预测得到的值与实际数值进行对比，计算MSE或者其他偏差，超出阈值则可认为属于异常。

4.1  SES（一次指数平滑）模型

从下式中可以看出来，SES中所有先前的观测值都对当前的平滑值产生了影响。

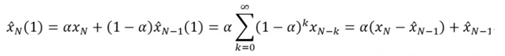
其中α表示平滑因子，值越大表示忽略时间距离较远的数值。时间序列比较平稳时，可以选择较小的α值，不同α的选择结果见图4。

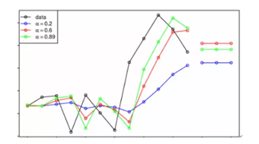
图4 SES模型不同α选择图示

4.2  Holt-Winters(三次指数平滑)模型

SES针对没有趋势和季节性的序列，二次指数平滑针对有趋势但是没有季节性的序列，Holt-Winters是三次指数平滑法，包含了周期和趋势性分量，和上面介绍的STL很像。其中S表示周期性分量，T表示趋势分量，L则表示残差分量。Xth用来预测h时刻的数值。公式中的s为周期长度，参数α、β和γ取值范围为[0,1]，表示趋势、周期等分量的占比。